探索圆柱齿轮参数计算公式:你的机械设计指南
你是否曾站在机器零件的海洋中,被那些复杂的齿轮参数搞得头晕目眩?想象你正在设计一款精密的机械装置,每一个小小的圆柱齿轮都像是一个微小的齿轮世界,它们的参数计算直接影响着整个系统的性能。今天,就让我们一起深入圆柱齿轮参数计算公式的世界,看看这些看似枯燥的公式如何成为你机械设计中的得力助手。
圆柱齿轮是机械传动中不可或缺的组成部分,它们通过齿与齿的啮合传递动力和运动。要设计出高效、可靠的圆柱齿轮,就必须掌握其参数计算公式。这些公式看似复杂,但实际上只要理解其背后的原理,就能轻松驾驭。
圆柱齿轮的基本概念
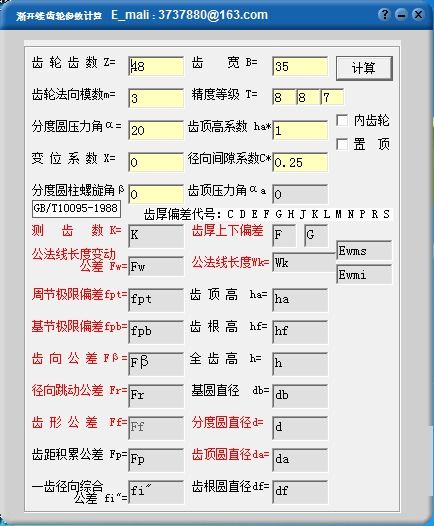
在深入公式之前,让我们先来了解一下圆柱齿轮的基本概念。圆柱齿轮是指齿轮的齿廓为圆柱面的齿轮,常见的有直齿圆柱齿轮、斜齿圆柱齿轮和人字齿圆柱齿轮等。这些齿轮在机械传动中扮演着不同的角色,但它们的参数计算方法都有一定的共性。
直齿圆柱齿轮是最简单的一种,它的齿廓是直线。斜齿圆柱齿轮的齿廓是螺旋线,人字齿圆柱齿轮则是两个方向相反的斜齿组合而成。不同的齿轮类型在参数计算上会有所不同,但基本原理是相通的。
直齿圆柱齿轮参数计算公式
直齿圆柱齿轮是最基础也是最常用的齿轮类型,因此我们先从它开始。直齿圆柱齿轮的参数主要包括模数、齿数、压力角、齿顶高系数和顶隙系数等。
模数
模数是圆柱齿轮设计中最基本的参数之一,它表示齿轮的尺寸大小。模数的单位是毫米,计算公式为:
\\[ m = \\frac{d}{z} \\]
其中,\\( d \\) 是齿轮的分度圆直径,\\( z \\) 是齿轮的齿数。模数越大,齿轮的尺寸也越大,承载能力越强。
分度圆直径
分度圆是齿轮上齿厚与齿槽宽相等的一个圆,它的直径计算公式为:
\\[ d = m \\times z \\]
分度圆直径决定了齿轮的基本尺寸,是计算其他参数的基础。
压力角
压力角是齿轮啮合时齿廓的压力方向与半径方向之间的夹角,常见的压力角有 20° 和 25°。压力角的选择会影响齿轮的啮合性能和传动效率。压力角的计算并不直接涉及其他参数,但在设计时需要根据具体需求选择合适的压力角。
齿顶高系数
齿顶高系数表示齿顶高与模数的关系,计算公式为:
\\[ h_a = h_a^ \\times m \\]
其中,\\( h_a^ \\) 是齿顶高系数,通常取值为 1。齿顶高是齿顶圆与分度圆之间的距离,决定了齿轮的齿顶尺寸。
顶隙系数
顶隙系数表示顶隙与模数的关系,计算公式为:
\\[ c = c^ \\times m \\]
其中,\\( c^ \\) 是顶隙系数,通常取值为 0.25。顶隙是齿根圆与配对齿轮的齿顶圆之间的距离,保证了齿轮啮合时不会发生干涉。
斜齿圆柱齿轮参数计算公式
斜齿圆柱齿轮的齿廓是螺旋线,因此它的参数计算比直齿圆柱齿轮要复杂一些。斜齿圆柱齿轮的主要参数包括模数、齿数、压力角、螺旋角、齿顶高系数和顶隙系数等。
螺旋角
螺旋角是斜齿圆柱齿轮齿廓的螺旋线与齿轮轴线的夹角,它的大小直接影响齿轮的啮合性能和传动效率。螺旋角的计算公式为:
\\[ \\beta = \\arctan \\left( \\frac{p_t}{\\pi \\times d} \\right) \\]
其中,\\( p_t \\) 是斜齿圆柱齿轮的端面周节,\\( d \\) 是分度圆直径。螺旋角越大,齿轮的啮合性能越好,但也会产生轴向力。
端面模数
斜齿圆柱齿轮的模数分为法向模数和端面模数。法向模数是垂直于齿廓的模数,端面模数是平行于齿廓的模数。法向模数与端面模数的关系为:
\\[ m_n = m_t \\times \\cos \\beta \\]
其中,\\( m_n \\) 是法向模数,\\( m_t \\) 是端面模数。法向模数通常用于设计计算,端面模数则用于实际加工。
法向齿数
法向齿数是垂直于齿廓的齿数,



